はじめに

これはJulia Advent Calendar 2019の20日目の記事です。「音について何か書きます」と宣言したので、普段Juliaを使って音についてどんなことをしているかを紹介します。今年はパワースペクトルの計算を、(1)信号全体をフーリエ変換する方法と、(2)スペクトログラムを時間平均する方法の2とおりでやってみます。

去年はAdvent Calendar参加記事として以下のようなものを書いていましたので、それからあまり進歩していませんが、ご容赦を。

marui.hatenablog.com

今回のエントリはJulia 1.0.5用に書いています。というのも、Julia 1.2や1.3あたりからLibSndFileなどのインストールがうまくいかない状況になっているからです。（原因はSampledSignals.jlにあるようですが、本稿を執筆している12月19日時点で解決されていません　→2019-12-31 解決しました）

julia> versioninfo()
Julia Version 1.0.5
Commit 3af96bcefc (2019-09-09 19:06 UTC)
Platform Info:
  OS: macOS (x86_64-apple-darwin18.6.0)
  CPU: Intel(R) Core(TM) i7-7920HQ CPU @ 3.10GHz
  WORD_SIZE: 64
  LIBM: libopenlibm
  LLVM: libLLVM-6.0.0 (ORCJIT, skylake)

パワースペクトルを自力で計算する

音あるいは時間信号のパワースペクトルは、信号をフーリエ変換して周波数ごとのパワーを抜き出したものです（位相成分は捨ててしまいます）。昨年のアドカレでは、DSP.jlを使用してスペクトログラムの計算をしましたが、その裏でどういった計算がされているのかについては紹介しませんでした。今年は、もう少し低レベルなやりかたを部分ごとに説明しながら書いてみようかと思います。

まずは下準備でいろいろとパッケージを読み込みます。

using FileIO: load   # ファイル読み込みのため
import LibSndFile    # 音ファイルの読み込みのため
using FFTW           # フーリエ変換
using DSP            # 信号処理
using Plots          # グラフを描きたい
pyplot()             # PlotsのバックエンドにはPyPlotを使う

手元にリコーダー演奏音のファイルがあるので、読み込みます。

julia> snd = load("recorder.flac")
352800-frame, 1-channel SampleBuf{FixedPointNumbers.Fixed{Int16,15}, 2}
8.0s sampled at 44100.0Hz
▁▅▅▅▅▅▅▅▅▅▅▅▅▅▅▅▅▂▁▁▁▁▁▁▁▁▁▁▁▁▅▅▅▅▅▆▆▆▆▆▆▆▆▆▆▆▆▅▁▁▁▁▁▁▁▁▁▁▁▅▅▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▅▁▁▁

snd構造体にはdataとsamplerateというフィールドが含まれており、それぞれサンプル単位のデータと標本化周波数となっています。量子化ビット数については、ファイルを読み込むときに[-1, +1)の範囲になるように変換してくれます。（つまり、2^(nbits-1)で除算された状態です）

julia> size(snd.data)
(352800, 1)

データ部分はサンプル数×チャンネル数の2次元配列になっています。今回はチャンネル数が1なので、モノラルデータで、length(snd.data) / snd.samplerateを実行すると8秒の長さだということも分かります。

今回のファイルには3回の吹鳴音が収録されているので、1チャンネル目の最初の2秒分のみを抜き出します。今回は列が一つしかありませんが、それでも2次元配列（行列）なので、vec(x)などとして行列からベクトルに変換することもできます。下のコードではx[start:end, 1]のような形式で1列だけを抜き出したのでsize(x)→(88200,)となります。

x = snd.data[1 : 2 * convert(Int, snd.samplerate), 1];

まずは波形を見てみましょう。

t = (0 : length(x)-1) / snd.samplerate;
plot(t, x, xlabel="Time (sec)", ylabel="Amplitude", legend=false)
savefig("plot_waveform.png")

ちょうど良く1音だけが含まれた状態になっています。

次は、この波形データをフーリエ変換して周波数スペクトルを見てみます。高速フーリエ変換（fft）をした結果には、各周波数ビンのスペクトル値が複素数で入っています。ここでは位相は無視して振幅部分だけを取り出しパワーに変換します（そのためにreal.(xx .* conj.(xx))では複素共役と掛け算をして実数部だけを取り出しています）。

xx = fft(x) / length(x);   # 高速フーリエ変換
xx = real.(xx .* conj.(xx));   # パワーにする
plot(xx, legend=false)
savefig("plot_spectrum1.png")

グラフが左右対称の形になっていることが分かります。これは、高速フーリエ変換では振幅スペクトルが以下のような配列で返ってくるからです。

長さNの信号を高速フーリエ変換すると、長さNの振幅スペクトルが返ります。配列の要素番号をJulia流に1〜Nとします。1番に入るDC成分（直流成分）は、0 Hzの振幅で、時間波形が正負どちらかにずれているとこの値が0以外になります。2〜N/2は各周波数ビン番号の振幅・位相が複素数で入っています。N/2+1番目はナイキスト周波数（サンプリング周波数の半分。この周波数以上の成分を保存することはできない）のデータが入っています。N/2+2番目〜N番目は、2〜N/2に入っていた成分の複素共役が逆順に入っています。このナイキストを超えた部分は負の周波数の成分です（以下の図のようにN/2+2番目以降を前に持ってくると、その雰囲気が分かります）。

正負の周波数にパワーが分かれた状態なので、それらを合算します。xx2にxxのDC〜ナイキスト成分をコピーし、そこにxxの後半を逆順に並べたものを加算することで実現しています。（じつはこの部分について、「正負に分かれたエネルギーを合算する」ことに納得いく説明を読んだことがないのですが（2021-12-02追記：日本音響学会誌の連載講座に振幅が半分になることの良い説明がありました。DOI: 10.20697/jasj.77.5_331の3.2節）、Matlabの公式サイトに10年ほど前に載っていたサンプルコードがそうしていたので踏襲しています）

xx2 = xx[1:div(length(xx), 2)+1];
xx2[2:div(length(xx), 2)] .+= reverse(xx[div(length(xx), 2)+2 : end]);
plot(xx2, legend=false)
savefig("plot_spectrum2.png")

横軸が周波数ビン番号のままなので、ちゃんと周波数を計算します。

f = (0 : length(xx2)) ./ length(xx2) .* (snd.samplerate / 2);
plot(f, xx2, xlabel="Frequency (Hz)", ylabel="Power", legend=false)
savefig("plot_spectrum3.png")

縦軸（パワー）をデシベル表示にしたいときには以下のようにします。

plot(f, 10*log10.(xx2),
     xlabel="Frequency (Hz)", ylabel="Power (dB)", legend=false)
savefig("plot_spectrum4.png")

横軸についても対数軸にしたい場合もあるでしょう。その場合はxscaleに:log10を渡してあげます。しかし、対数周波数では0 Hzが問題になってしまうので、ビン番号2以降のみを使用します。また、周波数軸の表示がデフォルトで10のべき乗になるので、自分が使いやすい周波数ラベル（xticks）にしています。

plot(f[2:end], 10*log10.(xx2[2:end]),
     xlabel="Frequency (Hz)", ylabel="Power (dB)",
     xscale=:log10, xlim=(20, 20000),
     xticks=((31, 63, 125, 250, 500, 1000, 2000, 4000, 8000, 16000),
             (31, 63, 125, 250, 500, 1000, 2000, 4000, 8000, 16000)),
     legend=false)
savefig("plot_spectrum5.png")

スペクトログラムを使う方法

DSP.jlにはperiodogramやspectrogramという関数があるので、それを利用することも可能です。ここではspectrogramを使ってみます。スペクトログラムは、時間信号を時間×周波数×パワーにするものです。昨年のアドカレで使い方は説明しているので、そのまま実行してみます。

winsize = 4096;
hopsize = 256;
S = spectrogram(x, winsize, winsize-hopsize, nfft=winsize*2,
                fs=snd.samplerate, window=hanning);

Sにはtime、freq、powerの3つのフィールドが入っています。この中でS.powerはlength(S.freq)×length(S.time)の2次元配列です。時間変化する信号でなければ、時間方向（S.powerの2次元目）で平均値を計算してパワースペクトルを得ることができます。ここでは縦軸をデシベルに変換して表示しています。

using Statistics
p = vec(mean(S.power, dims=2));
plot(S.freq, 10*log10.(p),
     xlabel="Frequency (Hz)", ylabel="Power (dB)", legend=false)
savefig("plot_spectrum6.png")

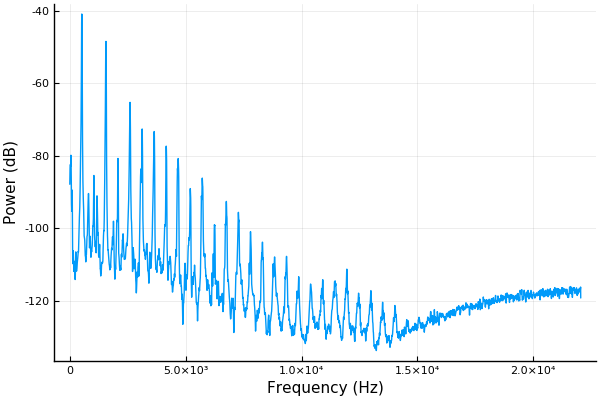
winsize、hopsize、nfftなどの引数を変えることで、どれだけ細かく分析をするのかなどを変えることができます。

まとめ

音信号のパワースペクトルを計算する方法として、(1)信号全体をフーリエ変換する方法と、(2)スペクトログラムを時間平均する方法を紹介しました。適材適所で使い分けがするとよいと思います。でわ！

~~（「正負に分かれたエネルギーを合算する」ことについて詳しい方がいましたら、コメントいただけると嬉しいです）~~

丸井綜研

パワースペクトル計算の2つの方法 (Julia Advent Calendar 2019)

はじめに

パワースペクトルを自力で計算する

スペクトログラムを使う方法

まとめ