簡単な統計ならすぐにできます。
julia> A = randn(5) #標準正規分布に従う乱数列を生成 [0.933857, 0.716588, 0.847243, 0.509315, 0.443582] julia> mean(A) # 平均 0.6901170571664779 julia> std(A) # 標準偏差 0.21110850675084233
正規分布の確率関数などは用意されていませんでしたが、関数は簡単に作れます。また、誤差関数は用意されているので、そこから累積密度関数も作れます。
julia> function normpdf(x) # 標準正規分布の確率密度関数
1 / sqrt(2pi) * exp(-x*x/2)
end
julia> function normcdf(x) # 標準正規分布の累積密度関数
(1 + erf(x/sqrt(2))) / 2
end
julia> normcdf(-2:0.1:2) # 作った関数を使ってみる
[0.0227501, 0.0287166, 0.0359303, 0.0445655 ... 0.96407, 0.971283, 0.97725]あとは累積密度関数の逆関数があれば、簡単な検定はすぐにできそうですね。
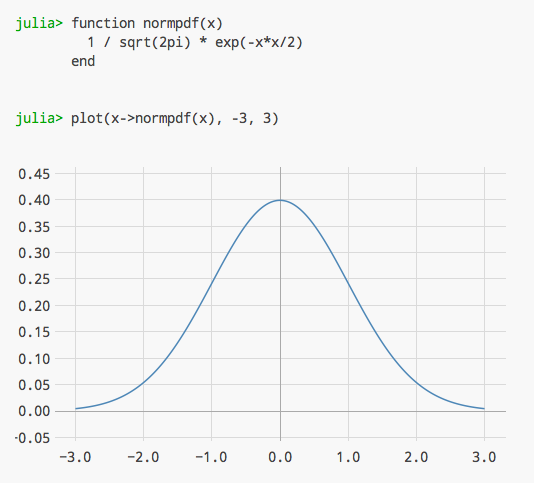
Juliaのウェブ・インターフェースを使えばグラフも書けます。
julia> plot(x->normpdf(x), -3, +3)