2021-09-24追記:正確に基音周波数が推定できない音があったので、別記事に対策を書きました。 →Juliaで基音周波数の推定(続き) - 丸井綜研
ピッチを感じる楽器の音は、基音と倍音とその他の成分音からなっています。どんな成分が入っているのか分析したいときには「楽器音の分析とスペクトログラム (Julia Advent Calendar 2018) - 丸井綜研」をぜひ。
ところで楽器音のピッチは基音の周波数と一致することが多いので、ピッチを知りたいときには基音の周波数を推定します。今日は基音の周波数を推定するためのごく簡単な方法を紹介します。
音を読み込む、処理する、可視化する、といったことをしたいので、必要なパッケージを読み込みます。
using FileIO: load import LibSndFile using DSP, FFTW using Plots pyplot();
音信号をファイルから読み込むのにはLibSndFile.load()を使います。今回はクラシックギターの1弦の開放音を読み込みます。
snd = load("guitar.wav")
読み込んだ信号の波形を見てみましょう。波形はsnd.data、標本化周波数はsnd.samplerateに入っていますが、名前が長いのでそれぞれxとfsに代入して使うことにします(モノラルファイルではない場合には1チャンネル目だけを使います)。tは各サンプルの時刻を秒単位であらわしたものです。
x = snd.data; if length(size(x)) > 1 x = x[:,1]; end fs = snd.samplerate; t = range(0, length(x)-1, step=1) ./ fs; plot(t, x, ylim=[-1, +1], xlabel="Time (sec)", ylabel="Amplitude", legend=false)
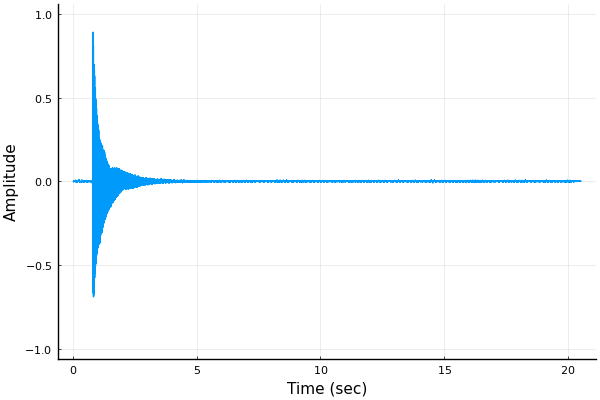
一回の撥弦音が収録されているのがわかります。
倍音成分を見るために、フーリエ変換を使って周波数スペクトルの計算をします。普通のFFTを使ってもいいのですが、負の周波数成分が出てこなくて手軽なFFTW.rfft()を使い、振幅を計算します。正確な振幅値を得るためには信号長で補正をかけたりするんですが、今回は振幅の絶対的な値には興味がないので無視します。fはスペクトルの各周波数ビンの中心周波数です。(普通のFFTを使った分析については「パワースペクトル計算の2つの方法 (Julia Advent Calendar 2019) - 丸井綜研」に書きました)
y = abs.(rfft(x)); f = range(0, stop=fs/2, length=length(y)); plot(f, y, xlabel="Frequency (Hz)", ylabel="Amplitude", legend=false)
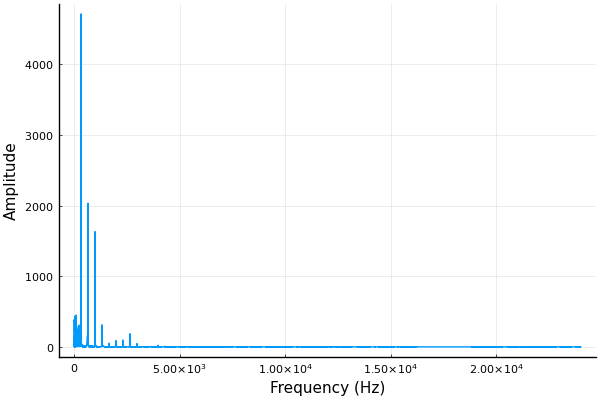
低い周波数に何本かピークがあるのがわかります。拡大表示してみましょう。
plot(f[1:50000], y[1:50000], xlabel="Frequency (Hz)", ylabel="Amplitude", legend=false)
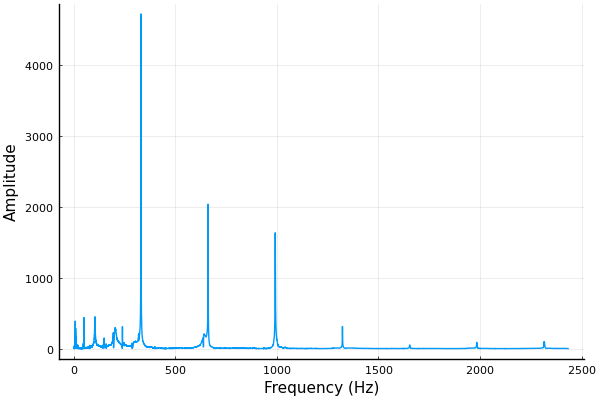
倍音成分が330 Hz付近、660Hz付近、990 Hz付近……に出ています。基音の成分が突出しているので、振幅が最大値になる周波数を求めれば基音周波数が推定できそうです。
(val, ind) = findmax(y)
f[ind]
とすると、330.96 Hzという結果でした。A4を440 Hzに合わせたとするとE4は329.6 Hzですから、だいたい正しい周波数が推定できてそうです。しかし、楽器によっては基音よりも第2倍音や第3倍音が振幅が大きい場合もあります。その場合、上記のようにスペクトルの最大値だけを見てしまうと、基音の周波数ではなく第2倍音や第3倍音の周波数を検出してしまいます。
そこで、スペクトルの自己相関関数を計算します。ピッチを持つ楽器では多くの場合、倍音成分は基音の整数倍の周波数にあらわれます。周波数軸上で等間隔に並んでいるので、自己相関を計算すればその周期を検出できるわけです。自己相関の計算には相互相関関数を使いますが、結果が対象になるので、片側半分だけを取り出します。
yc = xcorr(y, y); yc = yc[length(yc)÷2+1 : end]; yc = yc ./ maximum(yc); plot(f[1:50000], yc[1:50000], xlabel="Frequency (Hz)", ylabel="Correlation", legend=false)
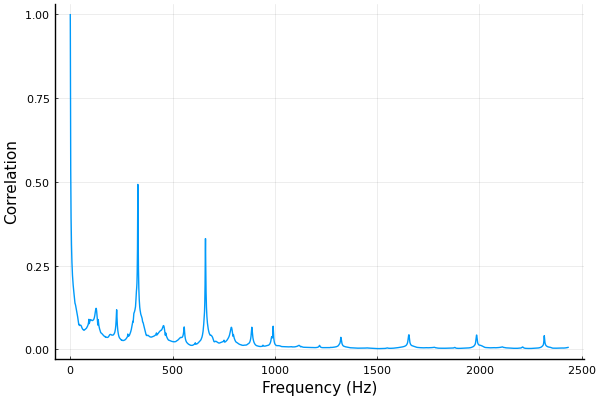
ちょうど330 Hz付近にピークがあります。自己相関なので当然ながらシフト量がゼロのときが相関最大になります。これを除去しないとfindmax()が使えませんので、下記のようにlowfreqという変数を用意して、その周波数以上の成分だけを検出対象にします。
lowfreq = 20; yc2 = yc[f .>= lowfreq]; fc2 = f[f .>= lowfreq]; (val, ind) = findmax(yc2); plot(fc2[ind-1000:ind+1000], yc2[ind-1000:ind+1000], xlabel="Frequency (Hz)", ylabel="Amplitude", legend=false)
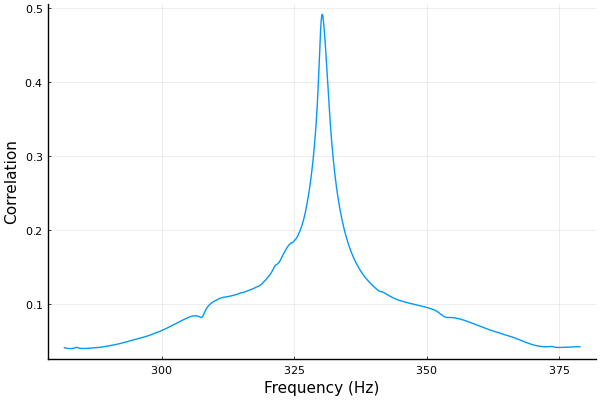
上のグラフは相関最大になった付近の拡大図です。もとのファイルの長さがけっこうあったので、FFTで得られたビン数も多く周波数分解能も高くなっています。ピークの周波数を見てみます。
fc2[ind]
結果、330.28 Hzと、基音周波数の推定ができました。
Juliaで手軽に基音周波数の推定をする簡単な方法を紹介しました。自分が手元で使っているコードでは、入力信号が短い場合はゼロ詰めして周波数分解能を上げるという処理を加えたものを関数化しています。
基音周波数推定は奥が深く、リアルタイム動作に適した洗練された方法も提案されていますので、興味がある方は調べてみてください。(たとえばDOI: 10.1121/1.1458024とかが有名です。「Juliaで基音周波数の推定(YINの解説)(Julia Advent Calendar 2021) - 丸井綜研」で解説してみました)