はじめに
僕は(電子音楽ではなくデスクトップミュージック の文脈での)コンピュータ音楽に触れるのが比較的はやく、NEC PC-8201 の内蔵ブザーを操作して単音シーケンサを作ったりしていました。高速アルペジオを使って和音もどきが出せるようになったときは嬉しかったです。
その後、NEC PC-9801シリーズでN88-BASICのMML (Music Macro Language) を使ってFM 3声 + SSG 3声(YM2203 - Wikipedia )を鳴らしたり、ローランドのミュージ郎 でMIDIの打ち込みをするようになったりしました。FM音源のときはMUSIC LALFというソフト*1 が、MIDIを使うようになってからはMusic NetworkのMicro Musican というソフトが僕のお気に入りでした。どちらのソフトもMMLを使うことができるというのが導入の大きな理由でした。特にMicro Musicianは譜面入力・ステップ入力・ピアノロール・MMLのあいだをシームレスに行ったり来たりできるソフトで、MMLで打ち込んだものが楽譜になるという、その柔軟さに驚いたものでした。(当時の主流はステップ入力のレコンポーザ でした)
大学に入ってからは、現在のApple Logic Pro X の先祖であるemagic 社のNotator LogicあたりをMacで触っていました。また、卒業研究では「MMLを使ってCGアニメーションを作るスクリプトを生成する」という研究をしました。音楽構造を視覚的な表現に変換するために、標準MIDIファイルを読み込んで、ノート番号やコントロールチェンジなどの情報をVRMLスクリプトに埋め込みました。MIDIファイルとVRMLを同期再生すると、音楽に合わせたアニメーションが見られるというわけです。その研究で使っていたのはPMMLという環境ですが、その発展形が以下の記事で紹介したTaktというプログラミング言語です。もう10年以上前の記事ですね……
marui.hatenablog.com
Pytaktが登場
その10年のあいだに、深層学習のためのインターフェース言語としてPythonが使われる事例が増え、それとともにPythonユーザーが爆発的に増えました。標準MIDIファイルを学習に使うといった用途の場合、MIDIで取得した音楽情報を扱うのにはTaktを使い、そこから出力したデータの統計分析や機械学習にはPythonを使うという使いわけが煩雑に感じられることもありました。Python用に開発されているpretty_midiやmusic21などのライブラリもありますしね。
そんな中、プログラミング言語Taktが形を変えて、PythonライブラリのPytaktとして提供されることになりました。プログラミング言語ではなくPythonライブラリなので、Taktそのものではありません。Python環境の中に埋め込まれるかたちで音楽情報を柔軟かつ高速に扱うことができる、Taktの思想を受け継いだライブラリです。もちろんMMLも使えるので、これまで通りに作編曲ツールとしても使えます(ストトン表記 にも対応!)。自動作曲や編曲支援のアルゴリズム部分はPythonで書き、その結果を標準MIDIファイルに書き出すのにPytaktを使うというのもありでしょう。
蛇足ですが、Takt同様にリアルタイム処理にも対応しており、MIDIエフェクタとしても使えます。現時点でのドキュメント類はPytakt論文 (DOI: 10.1080/09298215.2025.2540434 ) とAPIドキュメント くらいなので、本ブログでもシリーズ的に機能を見ていこうかと思っています。
Pytaktのインストール
Python環境は入っているものとします。PytaktはPyPIに登録されている ので、下記のようにすればダウンロード&インストールされます。アップデートも同じコマンドで大丈夫。*2
pip install -U pytakt
そのうえでPythonを立ち上げて、まずはMMLを触ってみましょう。
>>> import pytakt
>>> x = pytakt.mml("CDEFGAB^C" )
>>> x
EventList(duration=3840 , events=[
NoteEvent(t=0 , n=C4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=480 , n=D4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=960 , n=E4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=1440 , n=F4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=1920 , n=G4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=2400 , n=A4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=2880 , n=B4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=3360 , n=C5, L=480 , v=80 , nv=None , tk=1 , ch=1 )])
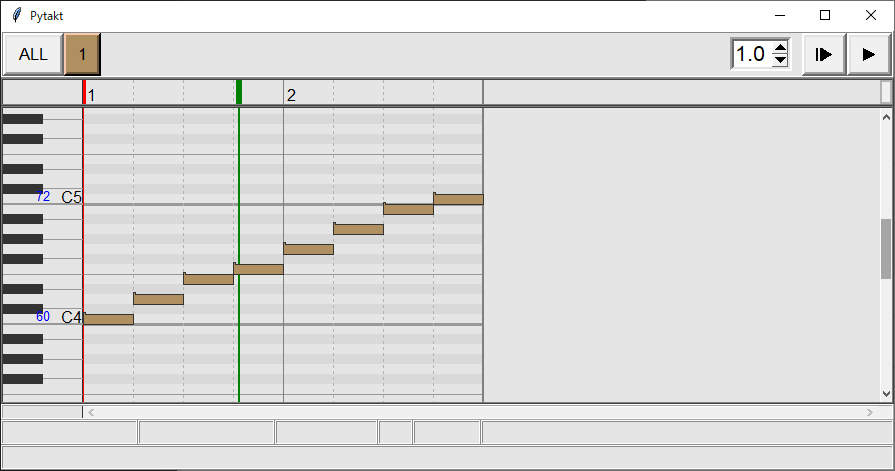
>>> x.show()
Pytakt内蔵のピアノロール・ビューア
mml()の中に音名を書くことで、NoteEventが生成されるのが分かります。NoteEventは音符ひとつをあらわすイベントで、開始時刻t、ノート番号n、音符長L、ノートオンヴェロシティv、トラック番号tk、チャンネル番号chなどが含まれています。それらがリスト (EventList) にまとめられています。最後にshow()命令でピアノロールを表示しています。ピアノロール画面では再生もできます。
開始時刻はティック単位で指定されます*3 。ノート番号は音高を指定するもので、PytaktではPython整数型を拡張したクラスとして作られています。異名同音を扱えるなど、ただのノート番号よりも機能が多いです。音符長は譜面上に書かれる音符記号としての長さを表します。実際にはスタッカートやテヌートなどで演奏時の音の長さは変わりますが、それは別途指定できるようになっています。
イベントリストに対して「4番目の音符のヴェロシティを変えたい」といった希望には以下のようにサクッと修正できます。
>>> x[3 ].update(v=120 )
NoteEvent(t=1440 , n=F4, L=480 , v=120 , nv=None , tk=1 , ch=1 )
また、なにかしらのMIDI音源が接続されていれば、play命令で再生できますし、標準MIDIファイルへの保存もwritesmfで一発です。
>>> x.play()
>>> x.writesmf("hoge.mid" )
他にもJSON、music21、pretty_midiといったフォーマットの読み書きもできるようになっていますので、例えば以下のようにすれば楽譜も得られます。(自分の環境ではMuse Score 3が自動的に起動しましたが、環境によってはうまくいかないかも)
>>> import pytakt
>>> import music21
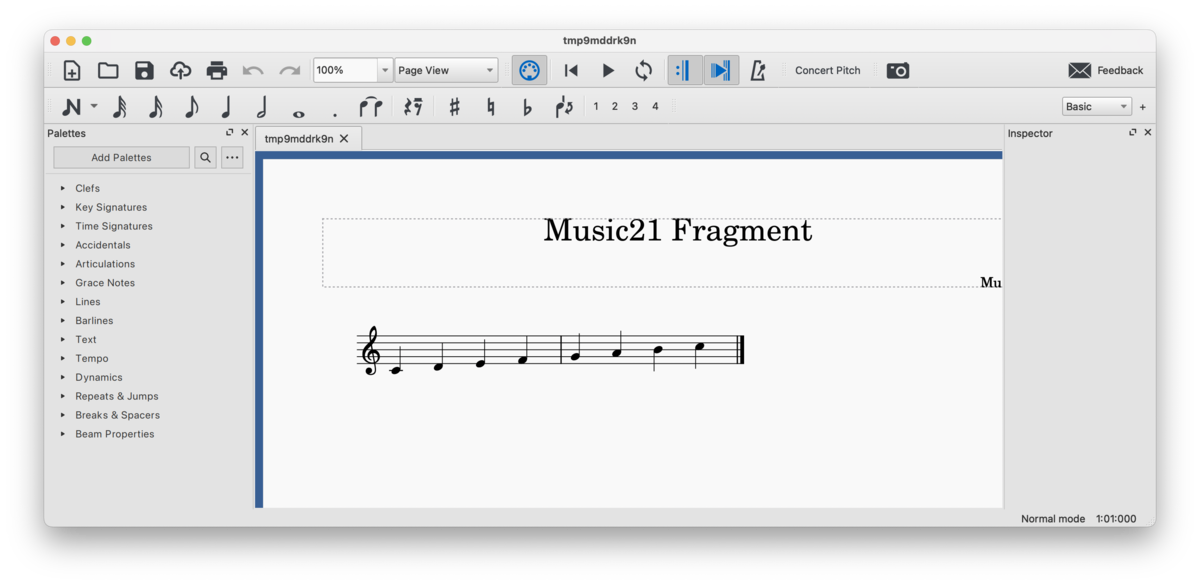
>>> pytakt.mml("CDEFGAB^C" ).music21().show()
music21を経由するとMuseScore 3で譜面表示ができます
Pytaktの簡単な紹介
いちいちpytakt.~と書くのが面倒なので、以下はfrom pytakt import *とした状態で実行しています。
音高と音程
絶対的な音の高さ(ピッチ)を表すPitchオブジェクトと、相対的な音高関係(つまり音程)をあらわすIntervalオブジェクトが用意されています。C4はノート番号60を表します。Cs4やDb4はノート番号61ですが、異名同音は文脈に応じて区別できるようになっているようです。音程はInterval('m3')(短3度)やInterval('a4')(増4度)などのように、M、m、a、d、Pが使えます。例えばC♯の短7度上を計算すると……Bになります。
>>> Cs4 + Interval('m7' )
B4
逆に、音高の引き算をしてみましょう。
>>> C5 - Ds4
Interval('d7' )
減7度 (diminish 7th) だと表示されます。長6度とか半音9個分ではなくちゃんと減7度となっているところからも、ただノート番号だけで計算しているわけではないことが分かります。((さらにはDb5 - Cs4を実行するとdd7が戻ってきます。))
音の連結と併合
音符はnote(音高, 長さ)で作成できます。2音以上の音符を時間方向に並べたいときは+で連結でき、和音にしたいときは&で併合します。
>>> note(C4, L4) + note(D4, L8)
EventList(duration=720 , events=[
NoteEvent(t=0 , n=C4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=480 , n=D4, L=240 , v=80 , nv=None , tk=1 , ch=1 )])
>>> note(C4, L4) & note(D4, L8)
EventList(duration=480 , events=[
NoteEvent(t=0 , n=C4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=0 , n=D4, L=240 , v=80 , nv=None , tk=1 , ch=1 )])
これをMMLで書く場合にはmml()を使います。和音にするには[~]です。
>>> mml('L4 C4 L8 D4' )
EventList(duration=720 , events=[
NoteEvent(t=0 , n=C4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=480 , n=D4, L=240 , v=80 , nv=None , tk=1 , ch=1 )])
>>> mml('[L4 C4 L8 D4]' )
EventList(duration=480 , events=[
NoteEvent(t=0 , n=C4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=0 , n=D4, L=240 , v=80 , nv=None , tk=1 , ch=1 )])
MML
さらにmml()を使っていきましょう。C D E F G A Bが基本の音名で、+または#がシャープ、-またはbがフラットを表します。ただし音名には小文字も使えるので、bbとなったら「シシ」なのか「シ♭」なのか区別ができません。そのためフラットにbを使うときには「シ」は大文字でBbと書きます。(調をハ短調に指定しておくとC D E F G A Bが自動的にC D Eb F G Ab Bbに変換される機能もあったりします)
休符はR、オクターブの指定は数字を使います(ピアノ中央のドC4がオクターブ番号の初期値)。オクターブの上下は^と_で指定します。
>>> mml('C E G ^C' )
EventList(duration=1920 , events=[
NoteEvent(t=0 , n=C4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=480 , n=E4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=960 , n=G4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=1440 , n=C5, L=480 , v=80 , nv=None , tk=1 , ch=1 )])
音の長さ(音価)はL8やL16などで直接指定できます(初期値はL4)が、「四分音符が並ぶ中に八分音符を入れたい」という場合には臨時記号として/(音価半分)と*(音価二倍)が使えます。また、~は「現在指定している音価を単位として延ばす」という意味になります。付点.も使えますし、特定の音符に対して音価を直接指定C(L8)することも可能です。
>>> mml('C D/ E// F* G** A~~ B.' )
EventList(duration=5880 , events=[
NoteEvent(t=0 , n=C4, L=480 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=480 , n=D4, L=240 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=720 , n=E4, L=120 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=840 , n=F4, L=960 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=1800 , n=G4, L=1920 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=3720 , n=A4, L=1440 , v=80 , nv=None , tk=1 , ch=1 ),
NoteEvent(t=5160 , n=B4, L=720 , v=80 , nv=None , tk=1 , ch=1 )])
おわりに(続きます)
記事が長くなってきたので、まずはここまで。このほかの膨大な機能については別記事にゆるゆると書いていきたいと思います。なによりMMLがPythonの中で書けるのが楽しいです。
北原鉄朗『音楽で身につけるディープラーニング』(オーム社, 2023年, amzn.to/4a4h1BW )ではpretty_midiを使っていますが、Pytaktで書き換えても面白いかもしれません。いつかやってみよう。